Simulating a simulation study

Introduction

In this vignette, we show how the simulated data included as an example dataset in simsum has been generated.

Motivation

Say we want to run a simulation study in which we want to compare the sensitivity of parametric and semiparametric survival models on relative risk estimates.

Data generating mechanisms

We simulate an hypothetical trial with a binary treatment. We fix the log-treatment effect to \(-0.50\), and we generate a treatment indicator variable for each simulated individual via a \(Binom(1, 0.5)\) random variable. We simulate two different sample sizes (50 and 250 individuals) and we assume two different baseline hazard functions: exponential with scale parameter \(\lambda = 0.5\), and Weibull with scale parameter \(\lambda = 0.5\) and shape parameter \(\gamma = 1.5\). Finally, we apply administrative censoring at time \(t = 5\).

exp_basehaz <- function(t, lambda = 0.5) lambda * 1 * t^0
exp_weibull <- function(t, lambda = 0.5, gamma = 1.5) lambda * gamma * t^(gamma - 1)
curve(exp_basehaz, from = 0, to = 5, lty = 1, ylim = c(0, 2), ylab = expression(h[0](t)), xlab = "Follow-up time t")
curve(exp_weibull, from = 0, to = 5, lty = 2, add = TRUE)
legend(x = "topleft", lty = 1:2, legend = c("Exponential baseline hazard", "Weibull baseline hazard"), bty = "n")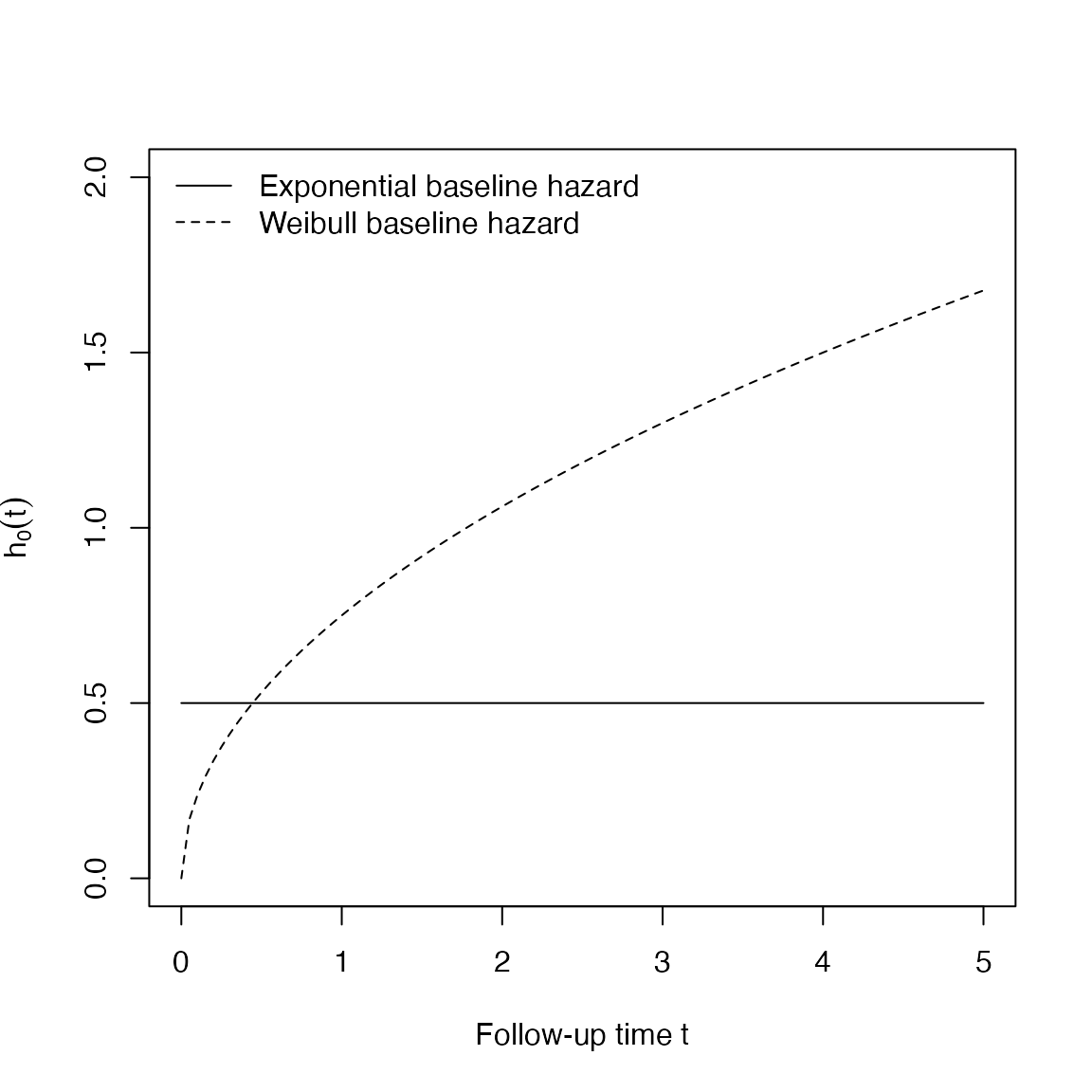

The survival times are estimated using the approach of Bender et al. (2005), based on drawing from a \(U(0, 1)\) random variable and applying the following transformations:

for an exponential baseline hazard, the survival time \(t\) is simulated as: \[t = -\frac{log(U)}{\lambda \exp(\beta ^ T X)}\]
for a Weibull baseline hazard, the survival time \(t\) is simulated as: \[t = \left(-\frac{log(U)}{\lambda \exp(\beta ^ T X)}\right) ^ {1 / \gamma}\]

The R function to simulate a dataset for our simulation study is defined as follows:

simulate_data <- function(dataset, n, baseline, params = list(), coveff = -0.50) {
  # Simulate treatment indicator variable
  x <- rbinom(n = n, size = 1, prob = 0.5)
  # Draw from a U(0,1) random variable
  u <- runif(n)
  # Simulate survival times depending on the baseline hazard
  if (baseline == "Exponential") {
    t <- -log(u) / (params$lambda * exp(x * coveff))
  } else {
    t <- (-log(u) / (params$lambda * exp(x * coveff)))^(1 / params$gamma)
  }
  # Winsorising tiny values for t (smaller than one day on a yearly-scale, e.g. 1 / 365.242), and adding a tiny amount of white noise not to have too many concurrent values
  t <- ifelse(t < 1 / 365.242, 1 / 365.242, t)
  t[t == 1 / 365.242] <- t[t == 1 / 365.242] + rnorm(length(t[t == 1 / 365.242]), mean = 0, sd = 1e-4)
  # ...and make sure that the resulting value is positive
  t <- abs(t)

  # Make event indicator variable applying administrative censoring at t = 5
  d <- as.numeric(t < 5)
  t <- pmin(t, 5)
  # Return a data.frame
  data.frame(dataset = dataset, x = x, t = t, d = d, n = n, baseline = baseline, stringsAsFactors = FALSE)
}

Methods

We compare the Cox model (Cox, 1972) with a fully parametric survival model assuming an exponential baseline hazard and a flexible parametric model with 2 degrees of freedom for modelling the baseline hazard (Royston and Parmar, 2002). The Cox model can be fit via the coxph function from the survival package, the exponential model can be fit via the phreg function from the eha package, and the Royston-Parmar model can be fixed via the stpm2 function from the rstpm2 package.

Performance measures

Say we are interested in the following performance measures:

Bias in the estimated log-treatment effect, and corresponding \(95\%\) Monte Carlo confidence intervals
Coverage of confidence intervals for the log-treatment effect, defined as the proportion of simulated data sets for which the true log-treatment effect of \(-0.50\) lies within the \(95\%\) confidence intervals obtained from the model

Sample size

We are primarily interested in bias, and assume that the variance of the estimated log-treatment effect is \(0.1\). The Monte Carlo standard error for the bias is:

\[\text{MCSE} = \sqrt{\frac{\text{variance}}{\# \text{simulations}}}\]

Aiming for a Monte Carlo standard error of 0.01 on the estimated bias, we would require \(1,000\) replications.

The Monte Carlo standard error for coverage is:

\[\text{MCSE} = \sqrt{\frac{\text{coverage} \times (1 - \text{coverage})}{\# \text{simulations}}}\]

This Monte Carlo standard error is maximised for a coverage = \(0.5\). In that setting, the Monte Carlo standard error with \(1,000\) replications would be \(0.01581139\), which is deemed to be acceptable.

Therefore, we should run \(1,000\) replications of this simulation study. However, for simplicity, we will run \(100\) replications only to speed up the process.

Running the simulation study

Generate data

We generate \(100\) datasets for each data-generating mechanism.

First, we set a random seed for reproducibility:

set.seed(755353002)

Then, we simulate the data:

reps <- 1:100
data <- list()
data[["n = 50, baseline = Exp"]] <- lapply(
  X = reps,
  FUN = simulate_data,
  n = 50,
  baseline = "Exponential",
  params = list(lambda = 0.5)
)
data[["n = 250, baseline = Exp"]] <- lapply(
  X = reps,
  FUN = simulate_data,
  n = 250,
  baseline = "Exponential",
  params = list(lambda = 0.5)
)
data[["n = 50, baseline = Wei"]] <- lapply(
  X = reps,
  FUN = simulate_data,
  n = 50,
  baseline = "Weibull",
  params = list(lambda = 0.5, gamma = 1.5)
)
data[["n = 250, baseline = Wei"]] <- lapply(
  X = reps,
  FUN = simulate_data,
  n = 250,
  baseline = "Weibull",
  params = list(lambda = 0.5, gamma = 1.5)
)

Run models

We define a function to fit the models of interest:

library(survival)
library(rstpm2)
#> Loading required package: splines
#> 
#> Attaching package: 'rstpm2'
#> The following object is masked from 'package:survival':
#> 
#>     colon

library(eha)

fit_models <- function(data, model) {
  # Fit model
  if (model == "Cox") {
    fit <- survival::coxph(Surv(t, d) ~ x, data = data)
  } else if (model == "RP(2)") {
    fit <- rstpm2::stpm2(Surv(t, d) ~ x, data = data, df = 2)
  } else {
    fit <- eha::phreg(Surv(t, d) ~ x, data = data, dist = "weibull", shape = 1)
  }
  # Return relevant coefficients
  data.frame(
    dataset = unique(data$dataset),
    n = unique(data$n),
    baseline = unique(data$baseline),
    theta = coef(fit)["x"],
    se = sqrt(ifelse(model == "Exp", fit$var["x", "x"], vcov(fit)["x", "x"])),
    model = model,
    stringsAsFactors = FALSE,
    row.names = NULL
  )
}

We now run the models for each simulated dataset:

results <- list()
results[["n = 50, baseline = Exp, model = Cox"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Exp"]],
    FUN = fit_models,
    model = "Cox"
  )
)
results[["n = 250, baseline = Exp, model = Cox"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Exp"]],
    FUN = fit_models,
    model = "Cox"
  )
)
results[["n = 50, baseline = Wei, model = Cox"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Wei"]],
    FUN = fit_models,
    model = "Cox"
  )
)
results[["n = 250, baseline = Wei, model = Cox"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Wei"]],
    FUN = fit_models,
    model = "Cox"
  )
)

results[["n = 50, baseline = Exp, model = Exp"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Exp"]],
    FUN = fit_models,
    model = "Exp"
  )
)
results[["n = 250, baseline = Exp, model = Exp"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Exp"]],
    FUN = fit_models,
    model = "Exp"
  )
)
results[["n = 50, baseline = Wei, model = Exp"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Wei"]],
    FUN = fit_models,
    model = "Exp"
  )
)
results[["n = 250, baseline = Wei, model = Exp"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Wei"]],
    FUN = fit_models,
    model = "Exp"
  )
)

results[["n = 50, baseline = Exp, model = RP(2)"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Exp"]],
    FUN = fit_models,
    model = "RP(2)"
  )
)
results[["n = 250, baseline = Exp, model = RP(2)"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Exp"]],
    FUN = fit_models,
    model = "RP(2)"
  )
)
results[["n = 50, baseline = Wei, model = RP(2)"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 50, baseline = Wei"]],
    FUN = fit_models,
    model = "RP(2)"
  )
)
results[["n = 250, baseline = Wei, model = RP(2)"]] <- do.call(
  rbind.data.frame,
  lapply(
    X = data[["n = 250, baseline = Wei"]],
    FUN = fit_models,
    model = "RP(2)"
  )
)

Aggregating results

relhaz <- do.call(
  rbind.data.frame,
  results
)
row.names(relhaz) <- NULL

We save the final results, that will be included as an example in the R package rsimsum.

library(usethis)
usethis::use_data(relhaz, overwrite = TRUE)

Summarising results

Finally, we obtain summary statistics by calling the simsum function:

library(rsimsum)
#> 
#> Attaching package: 'rsimsum'
#> The following object is masked _by_ '.GlobalEnv':
#> 
#>     relhaz

s <- rsimsum::simsum(data = relhaz, estvarname = "theta", se = "se", true = -0.50, methodvar = "model", ref = "Cox", by = c("n", "baseline"))
s
#> Summary of a simulation study with a single estimand.
#> True value of the estimand: -0.5 
#> 
#> Method variable: model 
#>  Unique methods: Cox, Exp, RP(2) 
#>  Reference method: Cox 
#> 
#> By factors: n, baseline 
#> 
#> Monte Carlo standard errors were computed.

summary(s)
#> Values are:
#>  Point Estimate (Monte Carlo Standard Error)
#> 
#> Non-missing point estimates/standard errors:
#>    n    baseline Cox Exp RP(2)
#>   50 Exponential 100 100   100
#>   50     Weibull 100 100   100
#>  250 Exponential 100 100   100
#>  250     Weibull 100 100   100
#> 
#> Average point estimate:
#>    n    baseline     Cox     Exp   RP(2)
#>   50 Exponential -0.4785 -0.4761 -0.4817
#>   50     Weibull -0.5282 -0.3491 -0.5345
#>  250 Exponential -0.5215 -0.5214 -0.5227
#>  250     Weibull -0.5120 -0.3518 -0.5139
#> 
#> Median point estimate:
#>    n    baseline     Cox     Exp   RP(2)
#>   50 Exponential -0.4507 -0.4571 -0.4574
#>   50     Weibull -0.5518 -0.3615 -0.5425
#>  250 Exponential -0.5184 -0.5165 -0.5209
#>  250     Weibull -0.5145 -0.3633 -0.5078
#> 
#> Average variance:
#>    n    baseline    Cox    Exp  RP(2)
#>   50 Exponential 0.1014 0.0978 0.1002
#>   50     Weibull 0.0931 0.0834 0.0898
#>  250 Exponential 0.0195 0.0191 0.0194
#>  250     Weibull 0.0174 0.0164 0.0172
#> 
#> Median variance:
#>    n    baseline    Cox    Exp  RP(2)
#>   50 Exponential 0.1000 0.0972 0.0989
#>   50     Weibull 0.0914 0.0825 0.0875
#>  250 Exponential 0.0195 0.0190 0.0194
#>  250     Weibull 0.0174 0.0164 0.0171
#> 
#> Bias in point estimate:
#>    n    baseline              Cox              Exp            RP(2)
#>   50 Exponential  0.0215 (0.0328)  0.0239 (0.0326)  0.0183 (0.0331)
#>   50     Weibull -0.0282 (0.0311)  0.1509 (0.0204) -0.0345 (0.0311)
#>  250 Exponential -0.0215 (0.0149) -0.0214 (0.0151) -0.0227 (0.0149)
#>  250     Weibull -0.0120 (0.0133)  0.1482 (0.0093) -0.0139 (0.0137)
#> 
#> Relative bias in point estimate:
#>    n    baseline              Cox              Exp            RP(2)
#>   50 Exponential -0.0430 (0.0657) -0.0478 (0.0652) -0.0366 (0.0662)
#>   50     Weibull  0.0564 (0.0623) -0.3018 (0.0408)  0.0690 (0.0622)
#>  250 Exponential  0.0430 (0.0298)  0.0427 (0.0301)  0.0455 (0.0298)
#>  250     Weibull  0.0241 (0.0267) -0.2963 (0.0186)  0.0279 (0.0274)
#> 
#> Empirical standard error:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.3285 (0.0233) 0.3258 (0.0232) 0.3312 (0.0235)
#>   50     Weibull 0.3115 (0.0221) 0.2041 (0.0145) 0.3109 (0.0221)
#>  250 Exponential 0.1488 (0.0106) 0.1506 (0.0107) 0.1489 (0.0106)
#>  250     Weibull 0.1333 (0.0095) 0.0929 (0.0066) 0.1368 (0.0097)
#> 
#> % gain in precision relative to method Cox:
#>    n    baseline             Cox                Exp            RP(2)
#>   50 Exponential 0.0000 (0.0000)    1.6773 (3.2902) -1.6262 (1.7888)
#>   50     Weibull 0.0000 (0.0000) 132.7958 (16.4433)  0.3583 (3.7387)
#>  250 Exponential 0.0000 (0.0000)   -2.3839 (3.0501) -0.1491 (0.9917)
#>  250     Weibull 0.0000 (0.0000) 105.8426 (12.4932) -4.9534 (2.0649)
#> 
#> Mean squared error:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.1073 (0.0149) 0.1056 (0.0146) 0.1089 (0.0154)
#>   50     Weibull 0.0968 (0.0117) 0.0640 (0.0083) 0.0969 (0.0117)
#>  250 Exponential 0.0224 (0.0028) 0.0229 (0.0028) 0.0225 (0.0028)
#>  250     Weibull 0.0177 (0.0027) 0.0305 (0.0033) 0.0187 (0.0028)
#> 
#> Model-based standard error:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.3185 (0.0013) 0.3127 (0.0010) 0.3165 (0.0012)
#>   50     Weibull 0.3052 (0.0014) 0.2888 (0.0005) 0.2996 (0.0012)
#>  250 Exponential 0.1396 (0.0002) 0.1381 (0.0002) 0.1394 (0.0002)
#>  250     Weibull 0.1320 (0.0002) 0.1281 (0.0001) 0.1313 (0.0002)
#> 
#> Relative % error in standard error:
#>    n    baseline              Cox               Exp            RP(2)
#>   50 Exponential -3.0493 (6.9011)  -4.0156 (6.8286) -4.4322 (6.8012)
#>   50     Weibull -2.0115 (6.9776) 41.4993 (10.0594) -3.6354 (6.8586)
#>  250 Exponential -6.2002 (6.6679)  -8.3339 (6.5160) -6.4133 (6.6528)
#>  250     Weibull -0.9728 (7.0397)  37.7762 (9.7917) -4.0199 (6.8228)
#> 
#> Coverage of nominal 95% confidence interval:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.9500 (0.0218) 0.9400 (0.0237) 0.9500 (0.0218)
#>   50     Weibull 0.9700 (0.0171) 0.9900 (0.0099) 0.9500 (0.0218)
#>  250 Exponential 0.9300 (0.0255) 0.9200 (0.0271) 0.9300 (0.0255)
#>  250     Weibull 0.9400 (0.0237) 0.8500 (0.0357) 0.9400 (0.0237)
#> 
#> Bias-eliminated coverage of nominal 95% confidence interval:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.9500 (0.0218) 0.9500 (0.0218) 0.9500 (0.0218)
#>   50     Weibull 0.9500 (0.0218) 1.0000 (0.0000) 0.9500 (0.0218)
#>  250 Exponential 0.9400 (0.0237) 0.9400 (0.0237) 0.9400 (0.0237)
#>  250     Weibull 0.9500 (0.0218) 0.9900 (0.0099) 0.9400 (0.0237)
#> 
#> Power of 5% level test:
#>    n    baseline             Cox             Exp           RP(2)
#>   50 Exponential 0.3600 (0.0480) 0.3800 (0.0485) 0.3700 (0.0483)
#>   50     Weibull 0.4300 (0.0495) 0.0900 (0.0286) 0.4700 (0.0499)
#>  250 Exponential 0.9800 (0.0140) 0.9900 (0.0099) 0.9900 (0.0099)
#>  250     Weibull 0.9700 (0.0171) 0.8600 (0.0347) 0.9700 (0.0171)

Conclusions

With this vignette we showed how to simulate survival data and run a small, simple simulation study.

References

Cox D.R. Regression models and life-tables. Journal of the Royal Statistical Society, Series B (Methodological), 1972, 34(2):187-220
Royston P. and Parmar M.K. Flexible parametric proportional-hazards and proportional-odds models for censored survival data, with application to prognostic modelling and estimation of treatment effects. Statistics in Medicine, 2002, 21(15):2175-2197
Bender R., Augustin T., and Blettner M. Generating survival times to simulate Cox proportional hazards models. Statistics in Medicine, 2005, 24(11):1713-1723

Alessandro Gasparini

2024-05-16